Solution 4.4:2b
From Förberedande kurs i matematik 1
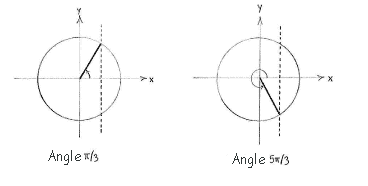
The equation \displaystyle \cos x= 1/2 has the solution \displaystyle x=\pi/3 in the first quadrant, and the symmetric solution \displaystyle x = 2\pi -\pi/3 = 5\pi/3 in the fourth quadrant.
If we add multiples of \displaystyle 2\pi to these two solutions, we obtain all the solutions
| \displaystyle x = \frac{\pi}{3}+2n\pi\qquad\text{and}\qquad x = \frac{5\pi }{3}+2n\pi\,, |
where n is an arbitrary integer.