Solution 4.3:6b
From Förberedande kurs i matematik 1
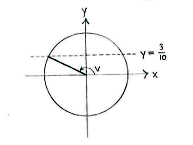
We draw an angle \displaystyle v in the unit circle, and the fact that \displaystyle \sin v = 3/10 means that its y-coordinate equals \displaystyle 3/10.
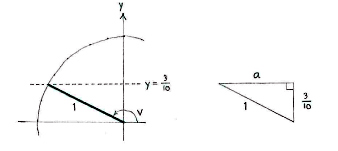
With the information that is given, we can define a right-angled triangle in the second quadrant which has a hypotenuse of 1 and a vertical side of length 3/10.
We can determine the triangle's remaining side by using the Pythagorean theorem,
| \displaystyle a^2 + \Bigl(\frac{3}{10}\Bigr)^2 = 1^2 |
which gives that
| \displaystyle a = \sqrt{1-\Bigl(\frac{3}{10}\Bigr)^2} = \sqrt{1-\frac{9}{100}} = \sqrt{\frac{91}{100}} = \frac{\sqrt{91}}{10}\,\textrm{.} |
This means that the angle's x-coordinate is \displaystyle -a, i.e. we have
| \displaystyle \cos v=-\frac{\sqrt{91}}{10} |
and thus
| \displaystyle \tan v = \frac{\sin v}{\cos v} = \frac{\dfrac{3}{10}}{-\dfrac{\sqrt{91}}{10}} = -\frac{3}{\sqrt{91}}\,\textrm{.} |