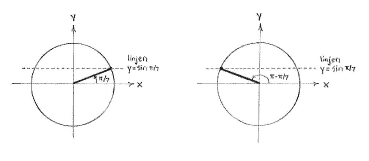
Solution 4.3:1b
From Förberedande kurs i matematik 1
Because the sine value for an angle is equal to the angle's y-coordinate on the unit circle, two angles have the same sine value only if they have the same y-coordinate. Therefore, if we draw in the angle \displaystyle \pi/7 on a unit circle, we see that the only angle between \displaystyle \pi/2 and \displaystyle \pi which has the same sine value lies in the second quadrant, where the line \displaystyle y = \sin (\pi/7) cuts the unit circle.
Because of symmetry, we have that this angle is the reflection of the angle \displaystyle \pi/7 in the y-axis, i.e. \displaystyle v = \pi - \pi/7 = 6\pi/7\,.