From Förberedande kurs i matematik 1

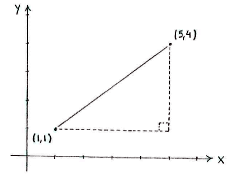
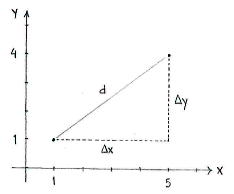
If we draw in the points in a coordinate system, we can see the line between the points as the hypotenuse in an imaginary right-angled triangle, where the opposite and adjacent are parallel with the x- and y-axes, respectively.

In this triangle, it is easy to measure the lengths of the opposite and the adjacent, which are simply the distances between the points in the x- and y-directions, respectively.

∆x = 5 - 1 = 4  and  ∆y = 4 - 1 = 3

Using the Pythagorean theorem, we can then calculate the length of the hypotenuse, which is also the distance between the points:

\displaystyle \begin{align} d &= \sqrt{(\Delta x)^2 + (\Delta y)^2} = \sqrt{4^2+3^2}\\[5pt] &= \sqrt{16+9} = \sqrt{25} = 5\,\textrm{.} \end{align}

Note: In general, the distance between two points \displaystyle (x,y) and \displaystyle (a,b) is given by the formula

\displaystyle d = \sqrt{(x-a)^2 + (y-b)^2}\,\textrm{.}