SamverkanFlervariabelanalysLIU
Övning 3.2.1
Skissa parablerna.
a) \displaystyle y=2(x+1)^2.
b) \displaystyle x=2y^2.
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Övning 3.2.2
Skissa ellipserna
a) \displaystyle 4x^2+\frac{1}{9}y^2=1.
b) \displaystyle \frac{(x+1)^2}{9}+\frac{(y-2)^2}{4}=1.
c) \displaystyle x^2+y^2+2x-4y=1
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Övning 3.2.3
Skissa hyperblerna
a) \displaystyle x^2-y^2=1.
b) \displaystyle 4x^2-\frac{1}{9}y^2=1.
c) \displaystyle 4x^2-\frac{1}{9}y^2=-1
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Övning 3.2.4
Rita följande mängder
a) \displaystyle \{(x,y)\in\mathbb{R}^2:\, 4x^2+\frac{1}{9}y^2<1\}.
b) \displaystyle \{(x,y)\in\mathbb{R}^2:\ 4x^2+\frac{1}{9}y^2\ge 1\}.
c) \displaystyle \{(x,y)\in\mathbb{R}^2:\, x\le 2y^2\}
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Övning 3.2.5
Rita följande mängder
a) \displaystyle \{(x,y)\in\mathbb{R}^2:\, x^2-y^2>1,\ 2x-y<3 ,\ x>0\}
b) \displaystyle \{(x,y\in\mathbb{R}^2:\, y< x,\ x^2+y^2\le 1\}
c) \displaystyle \{(x,y)\in\mathbb{R}^2:\, 4x^2+\frac{1}{9}y^2<1,\ y\ge -x\}
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Övning 3.2.6
Rita följande mängder
a) \displaystyle \{(x,y)\in\mathbb{R}^2:\, |x+y|\le 2 \}
b) \displaystyle \{(x,y\in\mathbb{R}^2:\, |x|+|y|\le 2\le 1\}
c) \displaystyle \{(x,y)\in\mathbb{R}^2:\, \max(|x|,|y|)\le 1\}
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Övning 3.2.7
Rita följande mängder
a) \displaystyle \{(x,y)\in\mathbb{R}^2:\, x^2+y^2<2<4-x^2-y^2+2x+4y\}
b) \displaystyle \{(x,y\in\mathbb{R}^2:\, 4\le x^2+y^2\le 9,\ x\le y\le 3x\}
c) \displaystyle \{(x,y)\in\mathbb{R}^2:\, x^2-y^2>4,\ x^2-y^2<9,\ xy>1,\ xy<4\}
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Övning 3.2.8
Bestäm randen, inre punkter och yttre punkter till mängderna i ??
Avgör också vilka av mängderna som är öppna, slutna och kompakta.
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Övning 3.2.9
Beskriv följande mängder analytiskt.
a) 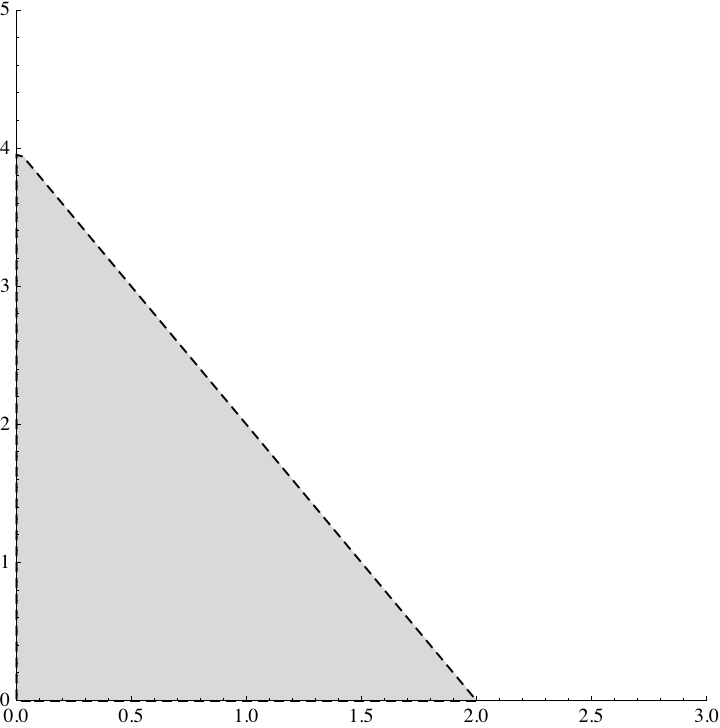
b) 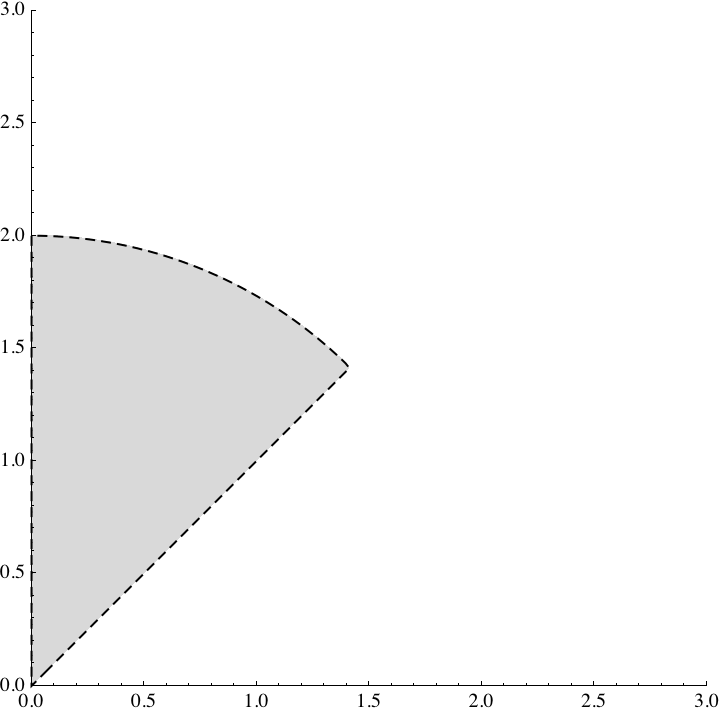
c) 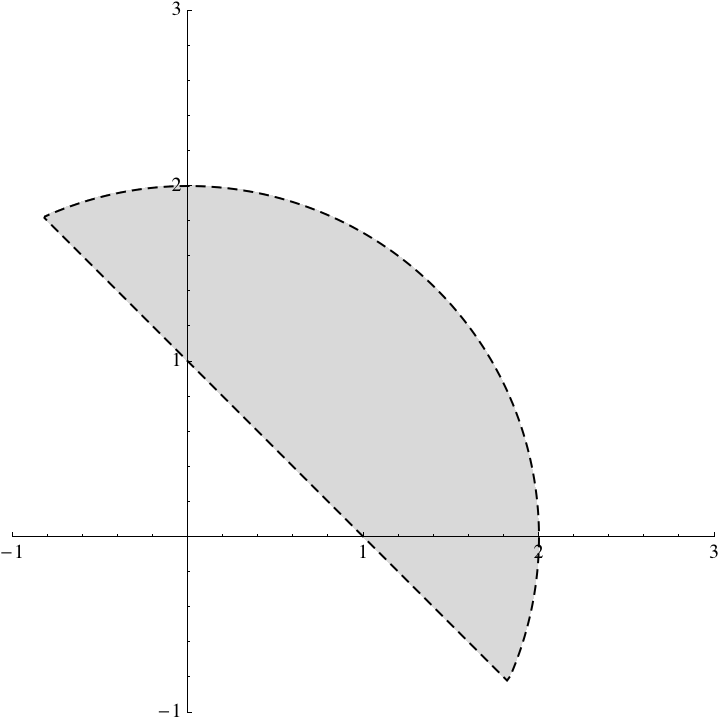
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
Visa mindre
Visa mer
Dölj allt
 Hämtar...
Hämtar...


