Svar Övning 9.1.2

SamverkanFlervariabelanalysLIU

(Skillnad mellan versioner)
Hoppa till: navigering, sök
Nuvarande version (16 september 2013 kl. 08.09) (redigera) (ogör)
 
(4 mellanliggande versioner visas inte.)
Rad 1: Rad 1:
a)
a)
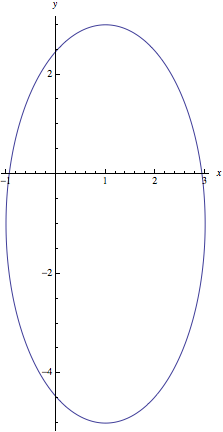
En ellips med centrum i <math>(1,-1)</math>: <math>(\frac{x-1}{2})^2+(\frac{y+1}{4})^2=1</math> en tangentvektor är <math>(0,-4)</math>
En ellips med centrum i <math>(1,-1)</math>: <math>(\frac{x-1}{2})^2+(\frac{y+1}{4})^2=1</math> en tangentvektor är <math>(0,-4)</math>
 +
 +
[[Bild:912a.png]]
b)
b)
-
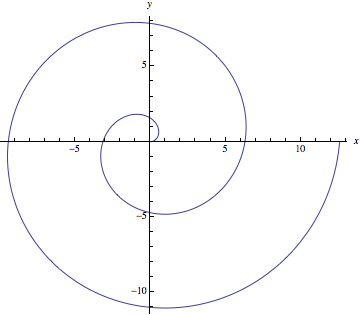
En spiral en tangentvektor är <math>(0,-\pi)</math>
+
En spiral, en tangentvektor är <math>(-1,-\pi)</math>
 +
 
 +
[[Bild:912b.png]]
c)
c)
-
Cirklar på cylindern <math>x^2+y^2=1</math> en tangentvektor är <math>(0,-1,1)</math>
+
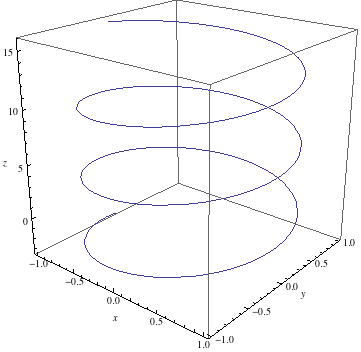
Kurva på cylindern <math>x^2+y^2=1</math> en tangentvektor är <math>(0,-1,1)</math>
 +
 
 +
[[Bild:912c.png]]

Nuvarande version

a) En ellips med centrum i \displaystyle (1,-1): \displaystyle (\frac{x-1}{2})^2+(\frac{y+1}{4})^2=1 en tangentvektor är \displaystyle (0,-4)

Bild:912a.png

b) En spiral, en tangentvektor är \displaystyle (-1,-\pi)

Bild:912b.png

c) Kurva på cylindern \displaystyle x^2+y^2=1 en tangentvektor är \displaystyle (0,-1,1)

Bild:912c.png

Den här artikeln är hämtad från http://wiki.sommarmatte.se/wikis/samverkan/flervariabelanalys-LIU/index.php/Svar_%C3%96vning_9.1.2