2.2 Mängder
SamverkanFlervariabelanalysLIU
| (En mellanliggande version visas inte.) | |||
| Rad 129: | Rad 129: | ||
b) <math>\{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z\le \sqrt{2-x^2-y^2}\}</math> | b) <math>\{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z\le \sqrt{2-x^2-y^2}\}</math> | ||
| - | c) <math>\{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z | + | c) <math>\{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z\le 1\}</math> |
d) <math>x+y+z=2,\ x^2+y^2+z^2= 2</math>. Om man lyser på kurvan från | d) <math>x+y+z=2,\ x^2+y^2+z^2= 2</math>. Om man lyser på kurvan från | ||
spetsen av <math>z</math>-axeln vad blir skuggan i <math>xy</math>-planet? | spetsen av <math>z</math>-axeln vad blir skuggan i <math>xy</math>-planet? | ||
| - | </div>{{#NAVCONTENT:Svar till a)|Svar Övning 3.2.11a|Svar till b)|Svar Övning 3.2.11b|Svar till c)|Svar Övning 3.2.11c|Tips och lösning till a)|Tips och lösning till övning 3.2.11a|Tips och lösning till b)|Tips och lösning till övning 3.2.11b|Tips och lösning till c)|Tips och lösning till övning 3.2.11c}} | + | </div>{{#NAVCONTENT:Svar till a)|Svar Övning 3.2.11a|Svar till b)|Svar Övning 3.2.11b|Svar till c)|Svar Övning 3.2.11c|Svar till d)|Svar Övning 3.2.11d|Tips och lösning till a)|Tips och lösning till övning 3.2.11a|Tips och lösning till b)|Tips och lösning till övning 3.2.11b|Tips och lösning till c)|Tips och lösning till övning 3.2.11c}} |
Nuvarande version
| 2.1 | 2.2 | 2.3 | 2.4 |
Innehåll |
Övning 3.2.2
Skissa ellipserna
a) \displaystyle 4x^2+\frac{1}{9}y^2=1.
b) \displaystyle \frac{(x+1)^2}{9}+\frac{(y-2)^2}{4}=1.
c) \displaystyle x^2+y^2+2x-4y=1
Övning 3.2.3
Skissa hyperblerna
a) \displaystyle x^2-y^2=1.
b) \displaystyle 4x^2-\frac{1}{9}y^2=1.
c) \displaystyle 4x^2-\frac{1}{9}y^2=-1
Övning 3.2.4
Rita följande mängder
a) \displaystyle \{(x,y)\in\mathbb{R}^2:\, 4x^2+\frac{1}{9}y^2<1\}.
b) \displaystyle \{(x,y)\in\mathbb{R}^2:\ 4x^2+\frac{1}{9}y^2\ge 1\}.
c) \displaystyle \{(x,y)\in\mathbb{R}^2:\, x\le 2y^2\}
Övning 3.2.5
Rita följande mängder
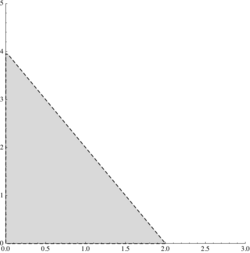
a) \displaystyle \{(x,y)\in\mathbb{R}^2:\, x^2-y^2>1,\ 2x-y<3 ,\ x>0\}
b) \displaystyle \{(x,y)\in\mathbb{R}^2:\, y< x,\ x^2+y^2\le 1\}
c) \displaystyle \{(x,y)\in\mathbb{R}^2:\, 4x^2+\frac{1}{9}y^2<1,\ y\ge -x\}
Övning 3.2.6
Rita följande mängder
a) \displaystyle \{(x,y)\in\mathbb{R}^2:\, |x+y|\le 2 \}
b) \displaystyle \{(x,y)\in\mathbb{R}^2:\, |x|+|y|\le 2\}
c) \displaystyle \{(x,y)\in\mathbb{R}^2:\, \max(|x|,|y|)\le 1\}
Övning 3.2.7
Rita följande mängder
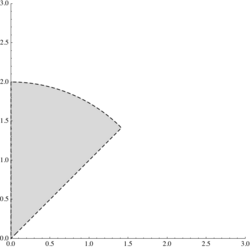
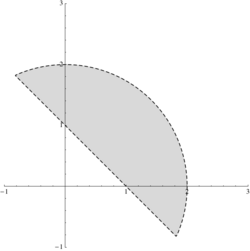
a) \displaystyle \{(x,y)\in\mathbb{R}^2:\, x^2+y^2<2<4-x^2-y^2+2x+4y\}
b) \displaystyle \{(x,y)\in\mathbb{R}^2:\, 4\le x^2+y^2\le 9,\ x\le y\le 3x\}
c) \displaystyle \{(x,y)\in\mathbb{R}^2:\, x^2-y^2>4,\ x^2-y^2<9,\ xy>1,\ xy<4\}
Övning 3.2.8
Bestäm randen, inre punkter och yttre punkter till mängderna i 3.2.4. Avgör också vilka av mängderna som är öppna, slutna och kompakta.
Övning 3.2.10
Rita följande mängder i \displaystyle \mathbb{R}^3
a) \displaystyle \{(x,y,z)\in\mathbb{R}^3:\, x+y+z\le 2,\ x\ge 0,\ y\ge 0,\ z\ge 0\}
b) \displaystyle \{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2+z^2= 1,\ z\ge 0,\ y>0\}
c) \displaystyle \{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2+z^2\le 1,\ z\ge 0,\ y>0\}
Övning 3.2.11
Rita följande mängder i \displaystyle \mathbb{R}^3
a) \displaystyle \{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z\le 2\}
b) \displaystyle \{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z\le \sqrt{2-x^2-y^2}\}
c) \displaystyle \{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z\le 1\}
d) \displaystyle x+y+z=2,\ x^2+y^2+z^2= 2. Om man lyser på kurvan från spetsen av \displaystyle z-axeln vad blir skuggan i \displaystyle xy-planet?
Övning 3.2.12
Beskriv mängderna
a) \displaystyle x=3\cos\theta,\ y=2\sin\theta då \displaystyle 0\le\theta\le\frac{\pi}{2}.
b) \displaystyle x=3\cos\theta,\ y=2\sin\theta då \displaystyle 0\le\theta\le\pi.
 Hämtar...
Hämtar...