2.2 Mängder
SamverkanFlervariabelanalysLIU
| Rad 118: | Rad 118: | ||
a) <math>\{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z\le 2\}</math> | a) <math>\{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z\le 2\}</math> | ||
| - | b) <math>\{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z\le \sqrt{2-x^2-y^2\}</math> | + | b) <math>\{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z\le \sqrt{2-x^2-y^2}\}</math> |
c) <math>\{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z^2\le 1\}</math> | c) <math>\{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z^2\le 1\}</math> | ||
Versionen från 19 mars 2012 kl. 10.02
Innehåll |
Övning 3.2.2
Skissa ellipserna
a) \displaystyle 4x^2+\frac{1}{9}y^2=1.
b) \displaystyle \frac{(x+1)^2}{9}+\frac{(y-2)^2}{4}=1.
c) \displaystyle x^2+y^2+2x-4y=1
Övning 3.2.3
Skissa hyperblerna
a) \displaystyle x^2-y^2=1.
b) \displaystyle 4x^2-\frac{1}{9}y^2=1.
c) \displaystyle 4x^2-\frac{1}{9}y^2=-1
Övning 3.2.4
Rita följande mängder
a) \displaystyle \{(x,y)\in\mathbb{R}^2:\, 4x^2+\frac{1}{9}y^2<1\}.
b) \displaystyle \{(x,y)\in\mathbb{R}^2:\ 4x^2+\frac{1}{9}y^2\ge 1\}.
c) \displaystyle \{(x,y)\in\mathbb{R}^2:\, x\le 2y^2\}
Övning 3.2.5
Rita följande mängder
a) \displaystyle \{(x,y)\in\mathbb{R}^2:\, x^2-y^2>1,\ 2x-y<3 ,\ x>0\}
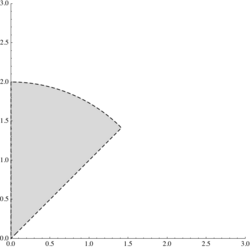
b) \displaystyle \{(x,y)\in\mathbb{R}^2:\, y< x,\ x^2+y^2\le 1\}
c) \displaystyle \{(x,y)\in\mathbb{R}^2:\, 4x^2+\frac{1}{9}y^2<1,\ y\ge -x\}
Övning 3.2.6
Rita följande mängder
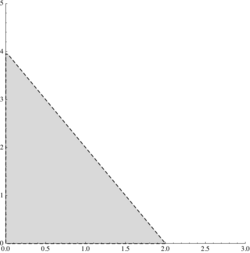
a) \displaystyle \{(x,y)\in\mathbb{R}^2:\, |x+y|\le 2 \}
b) \displaystyle \{(x,y)\in\mathbb{R}^2:\, |x|+|y|\le 2\le 1\}
c) \displaystyle \{(x,y)\in\mathbb{R}^2:\, \max(|x|,|y|)\le 1\}
Övning 3.2.7
Rita följande mängder
a) \displaystyle \{(x,y)\in\mathbb{R}^2:\, x^2+y^2<2<4-x^2-y^2+2x+4y\}
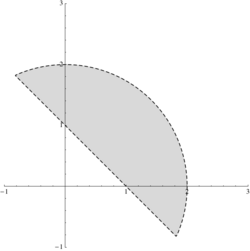
b) \displaystyle \{(x,y)\in\mathbb{R}^2:\, 4\le x^2+y^2\le 9,\ x\le y\le 3x\}
c) \displaystyle \{(x,y)\in\mathbb{R}^2:\, x^2-y^2>4,\ x^2-y^2<9,\ xy>1,\ xy<4\}
Övning 3.2.8
Bestäm randen, inre punkter och yttre punkter till mängderna i ?? Avgör också vilka av mängderna som är öppna, slutna och kompakta.
Övning 3.2.10
Rita följande mängder i \displaystyle \mathbb{R}^3
a) \displaystyle \{(x,y,z)\in\mathbb{R}^3:\, x+y+z\le 2,\ x\ge 0,\ y\ge 0,\ z\ge 0\}
b) \displaystyle \{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2+z^2= 1,\ z\ge 0,\ y>0\}
c) \displaystyle \{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2+z^2\le 1,\ z\ge 0,\ y>0\}
Övning 3.2.11
Rita följande mängder i \displaystyle \mathbb{R}^3
a) \displaystyle \{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z\le 2\}
b) \displaystyle \{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z\le \sqrt{2-x^2-y^2}\}
c) \displaystyle \{(x,y,z)\in\mathbb{R}^3:\, x^2+y^2\le z^2\le 1\}
d) \displaystyle x+y+z=2,\ x^2+y^2+z^2= 2. Om man lyser på kurvan från
spetsen av $z$-axeln vad blir skuggan i $xy$-planet?
 Hämtar...
Hämtar...