Solution 3.2:2d
From Förberedande kurs i matematik 2
(Difference between revisions)
(Ny sida: {{NAVCONTENT_START}} <center> Bild:3_2_2d.gif </center> {{NAVCONTENT_STOP}}) |
m |
||
| (4 intermediate revisions not shown.) | |||
| Line 1: | Line 1: | ||
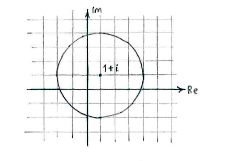
| - | {{ | + | In general, the expression <math>|z-w|</math> is equal to the distance between the complex numbers <math>z</math> and <math>w</math>, so if we rewrite the equality in the exercise as |
| - | < | + | |
| - | + | {{Displayed math||<math>|z-(1+i)|=3</math>}} | |
| + | |||
| + | it says that the distance between <math>z</math> and <math>1+i</math> should be 3, i.e. we obtain a circle of radius 3 and centre at <math>1+i</math>. | ||
| + | |||
| + | [[Image:3_2_2_d.gif|center]] | ||
Current revision
In general, the expression \displaystyle |z-w| is equal to the distance between the complex numbers \displaystyle z and \displaystyle w, so if we rewrite the equality in the exercise as
| \displaystyle |z-(1+i)|=3 |
it says that the distance between \displaystyle z and \displaystyle 1+i should be 3, i.e. we obtain a circle of radius 3 and centre at \displaystyle 1+i.