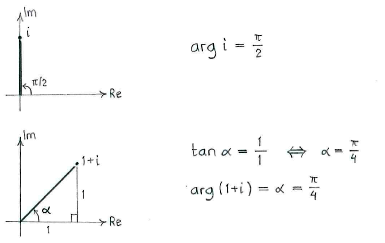Solution 3.2:5d

From Förberedande kurs i matematik 2

(Difference between revisions)
Jump to: navigation, search
m (Lösning 3.2:5d moved to Solution 3.2:5d: Robot: moved page)
Current revision (12:43, 29 October 2008) (edit) (undo)
m
 
(One intermediate revision not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
When dividing two complex numbers, the numerator's magnitude is divided by the denominator's magnitude and the numerator's argument is subtracted from the numerator's argument.
-
<center> [[Image:3_2_5d.gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
The argument of the quotient <math>i/(1+i)</math> is therefore
 +
 
 +
{{Displayed math||<math>\arg\frac{i}{1+i} = \arg i - \arg (1+i)\,\textrm{.}</math>}}
 +
 
 +
We obtain the argument of <math>i</math> and <math>1+i</math> by drawing the numbers in the complex plane and using a little trigonometry.
[[Image:3_2_5_d.gif|center]]
[[Image:3_2_5_d.gif|center]]
 +
 +
Hence, we obtain
 +
 +
{{Displayed math||<math>\arg\frac{i}{1+i} = \arg i - \arg (1+i) = \frac{\pi}{2} - \frac{\pi}{4} = \frac{\pi}{4}\,\textrm{.}</math>}}

Current revision

When dividing two complex numbers, the numerator's magnitude is divided by the denominator's magnitude and the numerator's argument is subtracted from the numerator's argument.

The argument of the quotient \displaystyle i/(1+i) is therefore

\displaystyle \arg\frac{i}{1+i} = \arg i - \arg (1+i)\,\textrm{.}

We obtain the argument of \displaystyle i and \displaystyle 1+i by drawing the numbers in the complex plane and using a little trigonometry.

Hence, we obtain

\displaystyle \arg\frac{i}{1+i} = \arg i - \arg (1+i) = \frac{\pi}{2} - \frac{\pi}{4} = \frac{\pi}{4}\,\textrm{.}
Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-ImperialCollege/index.php/Solution_3.2:5d"