Solution 2.1:1a
From Förberedande kurs i matematik 2
(Difference between revisions)
m |
|||
| (2 intermediate revisions not shown.) | |||
| Line 1: | Line 1: | ||
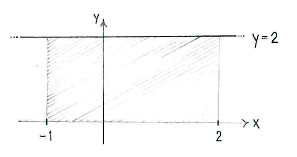
| - | + | The value of the integral can be interpreted as the area under the graph <math>y=2</math> from <math>x=-1\ </math> to <math>x=2</math>. | |
| - | < | + | |
| - | + | ||
| - | + | ||
[[Image:2_1_1_a.gif|center]] | [[Image:2_1_1_a.gif|center]] | ||
| + | |||
| + | Because the region is a rectangle, we can determine its area directly and obtain | ||
| + | |||
| + | {{Displayed math||<math>\int\limits_{-1}^{2} 2\,dx = \text{(base)}\cdot\text{(height)} = 3\cdot 2 = 6\,\textrm{.}</math>}} | ||
Current revision
The value of the integral can be interpreted as the area under the graph \displaystyle y=2 from \displaystyle x=-1\ to \displaystyle x=2.
Because the region is a rectangle, we can determine its area directly and obtain
| \displaystyle \int\limits_{-1}^{2} 2\,dx = \text{(base)}\cdot\text{(height)} = 3\cdot 2 = 6\,\textrm{.} |