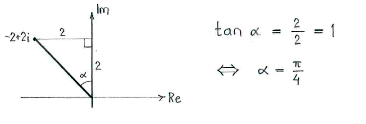Solution 3.2:5b

From Förberedande kurs i matematik 2

(Difference between revisions)
Jump to: navigation, search
m (Robot: Automated text replacement (-[[Bild: +[[Image:))
Current revision (12:29, 29 October 2008) (edit) (undo)
m
 
(2 intermediate revisions not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
The number <math>-2+2i</math> lies in the second quadrant and if we use an auxiliary triangle in that quadrant (according to the figure), we can use simple trigonometry to determine the angle <math>\alpha</math> which the line between the origin and
-
<center> [[Image:3_2_5b.gif]] </center>
+
<math>-2+2i</math> makes with the positive imaginary axis.
-
{{NAVCONTENT_STOP}}
+
[[Image:3_2_5_b1.gif|center]]
[[Image:3_2_5_b1.gif|center]]
 +
 +
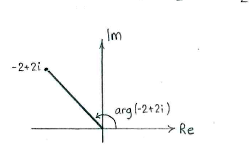
The argument of <math>-2+2i</math>, which is the angle to the positive real axis, therefore becomes
 +
 +
{{Displayed math||<math>\arg (-2+2i) = \frac{\pi}{2} + \alpha = \frac{\pi}{2} + \frac{\pi}{4} = \frac{3\pi}{4}\,\textrm{.}</math>}}
 +
[[Image:3_2_5_b2.gif|center]]
[[Image:3_2_5_b2.gif|center]]

Current revision

The number \displaystyle -2+2i lies in the second quadrant and if we use an auxiliary triangle in that quadrant (according to the figure), we can use simple trigonometry to determine the angle \displaystyle \alpha which the line between the origin and \displaystyle -2+2i makes with the positive imaginary axis.

The argument of \displaystyle -2+2i, which is the angle to the positive real axis, therefore becomes

\displaystyle \arg (-2+2i) = \frac{\pi}{2} + \alpha = \frac{\pi}{2} + \frac{\pi}{4} = \frac{3\pi}{4}\,\textrm{.}
Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-ImperialCollege/index.php/Solution_3.2:5b"