Solution 2.1:4a

From Förberedande kurs i matematik 2

(Difference between revisions)
Jump to: navigation, search
(Ny sida: {{NAVCONTENT_START}} <center> Bild:2_1_4a-1(2).gif </center> {{NAVCONTENT_STOP}} {{NAVCONTENT_START}} <center> Bild:2_1_4a-2(2).gif </center> {{NAVCONTENT_STOP}})
Current revision (13:36, 21 October 2008) (edit) (undo)
m
 
(4 intermediate revisions not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
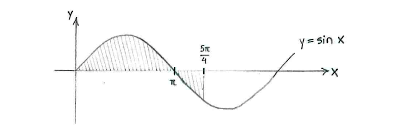
If we draw the curve <math>y=\sin x</math>, we see that the curve lies above the ''x''-axis as far as <math>x=\pi </math> and then lies under the ''x''-axis.
-
<center> [[Bild:2_1_4a-1(2).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
[[Image:2_1_4_a1.gif|center]]
-
{{NAVCONTENT_START}}
+
 
-
<center> [[Bild:2_1_4a-2(2).gif]] </center>
+
The area of the region between <math>x=0</math> and <math>x=\pi</math> can therefore be written as
-
{{NAVCONTENT_STOP}}
+
 
 +
{{Displayed math||<math>\int\limits_{0}^{\pi} \sin x\,dx</math>}}
 +
 
 +
whilst the area of the remaining region under the ''x''-axis is equal to
 +
 
 +
{{Displayed math||<math>-\int\limits_{\pi}^{5\pi/4} \sin x\,dx</math>}}
 +
 
 +
(note the minus sign in front of the integral).
 +
 
 +
The total area becomes
 +
 
 +
{{Displayed math||<math>\begin{align}
 +
& \int\limits_{0}^{\pi} \sin x\,dx - \int\limits_{\pi}^{5\pi/4} \sin x\,dx\\[5pt]
 +
&\qquad\quad {}= \Bigl[\ -\cos x\ \Bigr]_0^\pi - \Bigl[\ -\cos x\ \Bigr]_\pi^{5\pi/4}\\[5pt]
 +
&\qquad\quad {}= \Bigl( -\cos\pi - (-\cos 0)\Bigr) - \Bigl( -\cos\frac{5\pi}{4} - (-\cos\pi) \Bigr)\\[5pt]
 +
&\qquad\quad {}= \Bigl( -(-1)-(-1) \Bigr) - \Bigl( -\Bigl(-\frac{1}{\sqrt{2}} \Bigr) - \bigl(-(-1)\bigr)\Bigr)\\[5pt]
 +
&\qquad\quad {}= 1+1-\frac{1}{\sqrt{2}}+1\\[5pt]
 +
&\qquad\quad {}= 3-\frac{1}{\sqrt{2}}\,\textrm{.}
 +
\end{align}</math>}}
 +
 
 +
 
 +
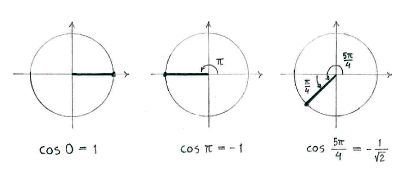
Note: A simple way to obtain the values of <math>\cos 0</math>, <math>\cos \pi </math> and <math>\cos (5\pi/4)</math> is to draw the angles <math>0</math>, <math>\pi</math> and <math>5\pi/4</math> on a unit circle and to read off the cosine value as the ''x''-coordinate for the corresponding point on the circle.
 +
 
 +
[[Image:2_1_4_a2.gif|center]]

Current revision

If we draw the curve \displaystyle y=\sin x, we see that the curve lies above the x-axis as far as \displaystyle x=\pi and then lies under the x-axis.

The area of the region between \displaystyle x=0 and \displaystyle x=\pi can therefore be written as

\displaystyle \int\limits_{0}^{\pi} \sin x\,dx

whilst the area of the remaining region under the x-axis is equal to

\displaystyle -\int\limits_{\pi}^{5\pi/4} \sin x\,dx

(note the minus sign in front of the integral).

The total area becomes

\displaystyle \begin{align}

& \int\limits_{0}^{\pi} \sin x\,dx - \int\limits_{\pi}^{5\pi/4} \sin x\,dx\\[5pt] &\qquad\quad {}= \Bigl[\ -\cos x\ \Bigr]_0^\pi - \Bigl[\ -\cos x\ \Bigr]_\pi^{5\pi/4}\\[5pt] &\qquad\quad {}= \Bigl( -\cos\pi - (-\cos 0)\Bigr) - \Bigl( -\cos\frac{5\pi}{4} - (-\cos\pi) \Bigr)\\[5pt] &\qquad\quad {}= \Bigl( -(-1)-(-1) \Bigr) - \Bigl( -\Bigl(-\frac{1}{\sqrt{2}} \Bigr) - \bigl(-(-1)\bigr)\Bigr)\\[5pt] &\qquad\quad {}= 1+1-\frac{1}{\sqrt{2}}+1\\[5pt] &\qquad\quad {}= 3-\frac{1}{\sqrt{2}}\,\textrm{.} \end{align}


Note: A simple way to obtain the values of \displaystyle \cos 0, \displaystyle \cos \pi and \displaystyle \cos (5\pi/4) is to draw the angles \displaystyle 0, \displaystyle \pi and \displaystyle 5\pi/4 on a unit circle and to read off the cosine value as the x-coordinate for the corresponding point on the circle.

Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-ImperialCollege/index.php/Solution_2.1:4a"