Aus Online Mathematik Brückenkurs 1

Zuerst schreiben wir alle Längen in dm (Dezimeter), damit wir in ganzen Zahlen arbeiten können.

Wir benennen die Abstände von den Bäumen zum Kleidungstück y und z, wie im Bild unten. Wir erhalten so zwei Dreiecke mit den Hypotenusen y und z (Wir haben angenommen, dass das Kleidungsstück schwer ist und alle Abstände gerade sind).

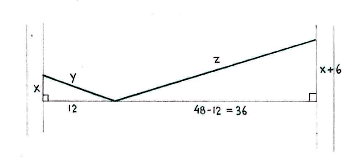
Nachdem die Wäscheleine 54 dm lang ist, erhalten wir

\displaystyle y+z=54\,\textrm{.}

(1)

Mit dem Gesetz des Pythagoras erhalten wir

\displaystyle y^2 = x^2 + 12^2\,,

(2)

\displaystyle z^2 = (x+6)^2 + 36^2\,\textrm{.}

(3)

Wir lösen jetzt die Gleichungen (1)-(3), indem wir zuerst z eliminieren, und eine Gleichung mit nur x und y erhalten. Danach eliminieren wir y, und erhalten so eine Gleichung mit nur x.

Von (1) erhalten wir \displaystyle z = 54-y, und dies in (3) ergibt

\displaystyle (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.}

(3')

Jetzt haben wir nurmehr die Gleichungen (2) und (3), und die Unbekannten x und y,

\displaystyle \left\{ \begin{align} & y^2 = x^2 + 12^2\,,\\[5pt] & (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.} \end{align} \right.

\displaystyle \begin{align}(2)\\[5pt] (3')\end{align}

Wir erweitern die Quadraten in (3'),

\displaystyle 54^2 - 2\cdot 54\cdot y + y^2 = x^2 + 2\cdot 6\cdot x + 6^2 + 36^2\,,

und vereinfachen

\displaystyle 2916 - 108y + y^2 = x^2 + 12x + 1332\,\textrm{.}

Wir verwenden (2) und ersetzen \displaystyle y^2 mit \displaystyle x^2+12 in dieser Gleichung

\displaystyle 2916 - 108y + x^2 + 144 = x^2 + 12x + 1332\,.

So eliminieren wir allex²-Terme:

\displaystyle 2916 - 108y + 144 = 12x + 1332\,.

Durch weitere Vereinfachung erhalten wir

\displaystyle 12x + 108y = 1728

(3")

Wir haben jetzt die Gleichungen (2) und (3') in die Gleichungen (2) und (3) gebracht, wobei (3) linear ist.

\displaystyle \left\{ \begin{align} & y^2 = x^2 + 12^2\,,\\[5pt] & 12x+108y=1728\,\textrm{.} \end{align} \right.

\displaystyle \begin{align}(2)\\[5pt] (3")\end{align}

Wir lösen y in der Gleichung (3"),

\displaystyle y=\frac{1728-12x}{108}=16-\frac{x}{9}

und ersetzen y mit \displaystyle 16-\frac{x}{9} in (2),

\displaystyle \Bigl(16-\frac{x}{9}\Bigr)^2 = x^2 + 144\,\textrm{.}

Dies ist eine Gleichung mit nur einer Unbekannten x. Diese lösen wir, indem wir zuerst die Quadrate auf der linken Seite erweitern:

\displaystyle 16^{2}-2\cdot 16\cdot \frac{x}{9} + \Bigl(\frac{x}{9} \Bigr)^2 = x^2 + 144\,.

Dann schreiben wir alle Terme auf eine Seite

\displaystyle x^2 - \frac{x^{2}}{81} + \frac{32}{9}x + 144 - 16^{2} = 0\,,

und erhalten damit

\displaystyle \frac{80}{81}x^2 + \frac{32}{9}x - 112 = 0\,\textrm{.}

Wir multiplizieren beide Seiten mit \displaystyle 81/80, damit wir die Gleichung auf Standardform bringen:

\displaystyle x^{2} + \frac{18}{5}x - \frac{567}{5} = 0\,\textrm{.}

Quadratische Ergänzung auf der linken Seite ergibt

\displaystyle \Bigl(x+\frac{9}{5}\Bigr)^2 - \Bigl(\frac{9}{5}\Bigr)^{2} - \frac{567}{5} = 0

oder

\displaystyle \Bigl(x+\frac{9}{5}\Bigr)^2 = \frac{81}{25} + \frac{567}{5} = \frac{2916}{25}\,,

also ist

\displaystyle x = -\frac{9}{5}\pm \sqrt{\frac{2916}{25}} = -\frac{9}{5}\pm \frac{54}{5}\,\textrm{.}

Also hat die Gleichung die Lösungen

\displaystyle x=-\frac{9}{5}-\frac{54}{5}=-\frac{63}{5}\qquad\text{und}\qquad x=-\frac{9}{5}+\frac{54}{5}=9\,\textrm{.}

Die Antwort ist also \displaystyle x=9\ \textrm{dm} (Die negative Lösung müssen wir verwerfen).

Um zu prüfen, ob wir richtig gerechnet haben, können wir zuerst y und z berechnen und testen, ob diese Werte zusammen mit x die Gleichungen (1) - (3) erfüllen.

Die Gleichung (3") gibt

\displaystyle y = 16-\frac{x}{9} = 16-1 = 15

und die Gleichung (1) gibt

\displaystyle z=54-y=54-15=39\,\textrm{.}

Jetzt prüfen wir, ob \displaystyle x=9, \displaystyle y=15 und \displaystyle z=39 die Gleichungen (1), (2) und (3) erfüllen:

\displaystyle \begin{align} \textrm{Linke Seite von (1)} &= 15+39 = 54\,,\\[5pt] \textrm{Rechte Seite von (1)} &= 54\,,\\[10pt] \textrm{Linke Seite von (2)} &= 15^2 = 225\,,\\[5pt] \textrm{Rechte Seite von (2)} &= 9^2 + 12^2 = 81+144 = 225\,,\\[10pt] \textrm{Linke Seite von (3)} &= 39^2 = 1521\,,\\[5pt] \textrm{Rechte Seite von (3)} &= (9+6)^2 + 36^2 = 15^2 + 36^2 = 225+1296 = 1521\,\textrm{.} \end{align}