Lösung 4.4:2e
Aus Online Mathematik Brückenkurs 1
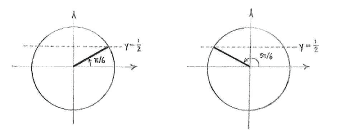
Diese Gleichung ist fast dieselbe wie in der vorigen Übung. Wir bestimmen zuerst die Winkel, die \displaystyle 0\le 5x\le 2\pi erfüllen durch den Einheitskreis:
| \displaystyle 5x = \frac{\pi}{6}\qquad\text{und}\qquad 5x = \pi - \frac{\pi}{6} = \frac{5\pi}{6}\,\textrm{.} |
Wir erhalten die allgemeine Lösung, indem wir ein Vielfaches von \displaystyle 2\pi zu den Lösungen addieren.
| \displaystyle 5x = \frac{\pi}{6} + 2n\pi\qquad\text{und}\qquad 5x = \frac{5\pi}{6} + 2n\pi\,, |
dividieren wir durch 5 und erhalten
| \displaystyle x = \frac{\pi}{30} + \frac{2}{5}n\pi\qquad\text{und}\qquad x = \frac{\pi}{6} + \frac{2}{5}n\pi\,, |