Aus Online Mathematik Brückenkurs 1

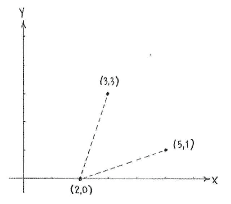
Die x-Achse besteht aus allen Punkten \displaystyle (x,0), wobei x die Unbekannte sei. Mit der Formel für den Abstand zwischen zwei Punkten erhalten wir den Abstand zwischen \displaystyle (x,0) und \displaystyle (3,3) sowie zwischen \displaystyle (5,1) und \displaystyle (x,0):

\displaystyle \sqrt{(x-3)^2+(0-3)^2}\qquad\text{und}\qquad \sqrt{(x-5)^2+(0-1)^2}\,\textrm{.}

Nachdem die beiden Abstände gleich sein sollen, erhalten wir:

\displaystyle \sqrt{(x-3)^2+9} = \sqrt{(x-5)^2+1}\,.

Wir quadrieren diese Gleichung und erhalten

\displaystyle (x-3)^2 + 9 = (x-5)^2+1\,\textrm{.}

Wir erweitern alle Terme und schreiben danach alle auf eine Seite,

\displaystyle \begin{align} & x^2-6x+9+9 = x^2-10x+25+1\\[5pt] &\quad\Leftrightarrow\quad 4x-8=0\,\textrm{.} \end{align}

Dies ergibt \displaystyle x=2, also ist der Punkt auf der x-Achse \displaystyle (2,0)\,.

Zum Schluss kontrollieren wir, ob die beiden Abstände auch wirklich gleich sind. Der Abstand zwischen \displaystyle (2,0) und \displaystyle (3,3) ist

\displaystyle \sqrt{(3-2)^2 + (3-0)^2} = \sqrt{1^2+3^2} = \sqrt{1+9} = \sqrt{10}

und der Abstand zwischen \displaystyle (2,0) und \displaystyle (5,1) ist

\displaystyle \sqrt{(5-2)^2 + (1-0)^2} = \sqrt{3^2 + 1^2} = \sqrt{9+1} = \sqrt{10}\,\textrm{.}

Hinweis: Obwohl wir unsere Gleichung quadriert haben, besteht kein Risiko Scheingleichungen zu erhalten, nachdem die Quadrate in der Wurzel immer positiv sind.