Aus Online Mathematik Brückenkurs 1

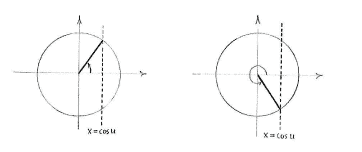
Für einen Konstanten u, ist die Gleichung

\displaystyle \cos u=\cos v

für folgende Winkeln v erfüllt

\displaystyle v=u\qquad\text{und}\qquad v=-u\,\textrm{.}

Also sind die allgemeinen Lösungen

\displaystyle v=u+2n\pi\qquad\text{und}\qquad v=-u+2n\pi\,,

Also hat die Gleichung

\displaystyle \cos 5x=\cos (x+\pi/5)

die Lösungen

\displaystyle \left\{\begin{align} 5x&=x+\frac{\pi}{5}+2n\pi\quad\text{oder}\\[5pt] 5x &= -x-\frac{\pi}{5}+2n\pi\,\textrm{.}\end{align}\right.

Lösen wir die Gleichung für x, erhalten wir

\displaystyle \left\{\begin{align} x &= \frac{\pi}{20} + \frac{n\pi}{2}\,,\\[5pt] x &= -\frac{\pi }{30}+\frac{n\pi}{3}\,, \end{align}\right.