Aus Online Mathematik Brückenkurs 1

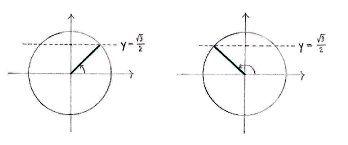
Wir zeichnen den Einheitskreis, und markieren alle Winkeln die die 'y-Koordinate \displaystyle \sqrt{3}/2 haben. So erhalten wir alle Lösungen der Gleichung zwischen \displaystyle 0 und \displaystyle 2\pi.

Im ersten Quadrant wissen wir dass \displaystyle x = \pi/3 den Sinus \displaystyle \sqrt{3}/2 hat. Noch dazu hat die Spiegelung in der y-Achse denselben Sinus, und also ist \displaystyle x = \pi - \pi/3 = 2\pi/3 auch eine Lösung.

Addieren wir einen Multipel von \displaystyle 2\pi zu irgendeiner dieser Winkeln, ändert sich nicht deren Sinus.

\displaystyle x = \frac{\pi}{3}+2n\pi\qquad\text{und}\qquad x = \frac{2\pi}{3}+2n\pi\,,

wo n eine beliebige ganze Zahl ist.

Hinweis: Schreiben wir

\displaystyle x = \frac{\pi}{3}+2n\pi\qquad\text{und}\qquad x = \frac{2\pi}{3}+2n\pi\,\textrm{,}

heißt dies dass die Gleichung für jedes n erfüllt ist, und also für die Winkeln:

\displaystyle \begin{array}{llll} &n=0:\quad &x=\frac{\pi}{3}\quad &x=\frac{2\pi }{3}\\[5pt] &n=-1:\quad &x=\frac{\pi}{3}+(-1)\cdot 2\pi\quad &x=\frac{2\pi}{3}+(-1)\cdot 2\pi\\[5pt] &n=1:\quad &x=\frac{\pi}{3}+1\cdot 2\pi\quad &x=\frac{2\pi}{3}+1\cdot 2\pi\\[5pt] &n=-2:\quad &x=\frac{\pi}{3}+(-2)\cdot 2\pi\quad &x=\frac{2\pi}{3}+(-2)\cdot 2\pi\\[5pt] &n=2:\quad &x=\frac{\pi}{3}+2\cdot 2\pi\quad &x=\frac{2\pi}{3}+2\cdot 2\pi\\[5pt] &\phantom{n}\vdots &\phantom{x}\vdots &\phantom{x}\vdots \end{array}