Aus Online Mathematik Brückenkurs 1

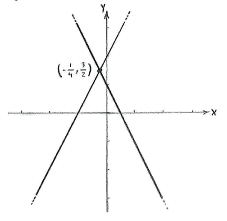
Der Schnittpunkt der Geraden muss die Gleichungen beider Geraden erfüllen

\displaystyle 2x+y-1=0\qquad\text{and}\qquad y-2x-2=0\,\textrm{.}

Wenn wir von der ersten Gleichung \displaystyle y mit \displaystyle 2x+2 ersetzen, bekommen wir eine Gleichung mit nur \displaystyle x

\displaystyle 2x+(2x+2)-1=0\quad\Leftrightarrow\quad 4x+1=0\,,

Wir erhalten \displaystyle x=-1/4\,, und die erste Gleichung, \displaystyle y=2x+2, gibt uns \displaystyle y = 2\cdot(-1/4)+2 = 3/2\,.

Also ist der Schnittpunkt \displaystyle \bigl(-\tfrac{1}{4},\tfrac{3}{2}\bigr).

Wir kontrollieren zur Sicherheit dass der Punkt \displaystyle \bigl(-\tfrac{1}{4},\tfrac{3}{2}\bigr) auch wirklich beide Gleichungen erfüllt

• 2x + y - 1 = 0: \displaystyle \quad\textrm{Linke Seite} = 2\cdot\bigl(-\tfrac{1}{4}\bigr) + \tfrac{3}{2} - 1 = -\tfrac{1}{2} + \tfrac{3}{2} - \tfrac{2}{2} = 0 = \textrm{Rechte Seite.}

• y - 2x - 2 = 0: \displaystyle \quad\textrm{Linke Seite} = \tfrac{3}{2}-2\cdot\bigl(-\tfrac{1}{4}\bigr)-2 = \tfrac{3}{2} + \tfrac{1}{2} - \tfrac{4}{2} = 0 = \textrm{Rechte Seite.}