Aus Online Mathematik Brückenkurs 1

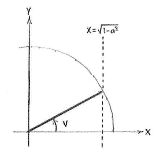
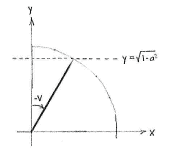
The expression for the angle \displaystyle \pi/2 - v differs from \displaystyle \pi/2 by as much as \displaystyle -v differs from \displaystyle 0. This means that \displaystyle \pi/2-v makes the same angle with the positive y-axis as \displaystyle -v makes with the positive x-axis.

Angle v		Angle π/2 - v

Therefore, the angle \displaystyle \pi/2 - v has a y-coordinate which is equal to the x-coordinate for the angle v, i.e.

\displaystyle \sin\Bigl(\frac{\pi}{2} - v\Bigr) = \cos v

and from exercise c, we know that \displaystyle \cos v = \sqrt{1-a^2}\,,

\displaystyle \sin\Bigl(\frac{\pi}{2}-v\Bigr) = \sqrt{1-a^2}\,\textrm{.}