Lösung 4.3:9
Aus Online Mathematik Brückenkurs 1
Using the formula for double angles on \displaystyle \sin 160^{\circ} gives
On the right-hand side, we see that the factor \displaystyle \cos 80^{\circ} has appeared, and if we use the formula for double angles on the second factor (\displaystyle \sin 80^{\circ}),
we obtain a further factor \displaystyle \cos 40^{\circ}. A final application of the formula for double angles on \displaystyle \sin 40^{\circ } gives us all three cosine factors,
We have thus succeeded in showing that
which can also be written as
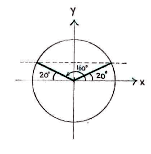
If we draw the unit circle, we see that \displaystyle 160^{\circ} makes an angle of \displaystyle 20^{\circ} with the negative x-axis, and therefore the angles \displaystyle 20^{\circ} and \displaystyle 160^{\circ} have the same y-coordinate in the unit circle, i.e.
This shows that