Lösung 4.1:4c
Aus Online Mathematik Brückenkurs 1
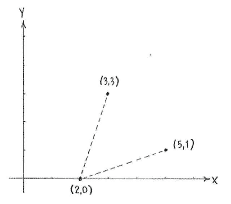
Let the point on the x-axis have coordinates \displaystyle (x,0), where x is an unknown number. Then, using the distance formula, the distance from the point \displaystyle (x,0) to \displaystyle (3,3) and \displaystyle (5,1) is given by
respectively. Because these two distances should be the same, we get the equation
or, if we take the square, so as to get rid of the square root sign,
Now, expand the squares and collect together all the terms onto one side,
This gives that \displaystyle x=2, i.e. the point on the x-axis is \displaystyle (2,0)\,.
As a final step, we check that we have calculated correctly and that the distances really are the same. The distance between \displaystyle (2,0) and \displaystyle (3,3)
is
and the distance between \displaystyle (2,0) and \displaystyle (5,1) is
Note: Although we squared our root equation, it is not in fact necessary to test the solution for that reason, because the expressions under the root signs are sums of squares which are never negative and therefore cannot give rise to so-called spurious roots.