Lösung 4.4:2b
Aus Online Mathematik Brückenkurs 1
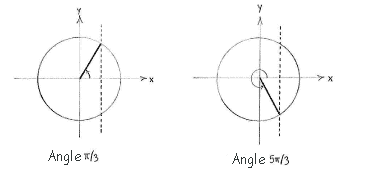
The equation \displaystyle \cos x={1}/{2}\; has the solution \displaystyle x={\pi }/{3}\; in the first quadrant, and the symmetric solution \displaystyle x={2\pi -\pi }/{3}\;={5\pi }/{3}\; in the fourth quadrant.
Angle \displaystyle {\pi }/{3}\; Angle \displaystyle {5\pi }/{3}\;
If we add multiples of
\displaystyle 2\pi
to these two solutions, we obtain all the solutions
\displaystyle x={\pi }/{3}\;+2n\pi
and
\displaystyle x={5\pi }/{3}\;+2n\pi
where
\displaystyle n
is an arbitrary integer.