Aus Online Mathematik Brückenkurs 1

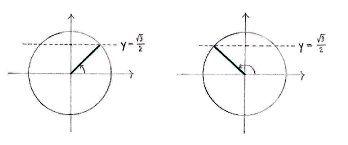
We draw a unit circle and mark on those angles on the circle which have a \displaystyle y -coordinate of \displaystyle {\sqrt{3}}/{2}\;, in order to see which solutions lie between \displaystyle 0 and \displaystyle 2\pi .

In the first quadrant, we recognize \displaystyle x={\pi }/{3}\; as the angle which has a sine value of \displaystyle {\sqrt{3}}/{2}\; and then we have the reflectionally symmetric solution \displaystyle x=\pi -\frac{\pi }{3}=\frac{2\pi }{3} in the second quadrant.

Each of those solutions returns to itself after every revolution, so that we obtain the complete solution if we add multiples of \displaystyle 2\pi

\displaystyle x=\frac{\pi }{3}+2n\pi and \displaystyle x=\frac{2\pi }{3}+2n\pi

where \displaystyle n is an arbitrary integer.

NOTE: when we write that the complete solution is given by

\displaystyle x=\frac{\pi }{3}+2n\pi and \displaystyle x=\frac{2\pi }{3}+2n\pi ,

this means that for every integer \displaystyle n, we obtain a solution to the equation:

\displaystyle \begin{array}{*{35}l} n=0 & x=\frac{\pi }{3} & x=\frac{2\pi }{3} \\ n=-1 & x=\frac{\pi }{3}+\left( -1 \right)\centerdot 2\pi & x=\frac{2\pi }{3}+\left( -1 \right)\centerdot 2\pi \\ n=1 & x=\frac{\pi }{3}+1\centerdot 2\pi & x=\frac{2\pi }{3}+1\centerdot 2\pi \\ n=-2 & x=\frac{\pi }{3}+\left( -2 \right)\centerdot 2\pi & x=\frac{2\pi }{3}+\left( -2 \right)\centerdot 2\pi \\ n=2 & x=\frac{\pi }{3}+2\centerdot 2\pi & x=\frac{2\pi }{3}+2\centerdot 2\pi \\ \end{array}

and so on.