Aus Online Mathematik Brückenkurs 1

Because \displaystyle \tan v=\frac{\sin v}{\cos v}, the condition \displaystyle \text{tan }v=\text{1 } gives \displaystyle \text{sin }v=\text{ cos }v, i.e. we look for angles in the unit circle whose \displaystyle x - and \displaystyle y -coordinates are equal.

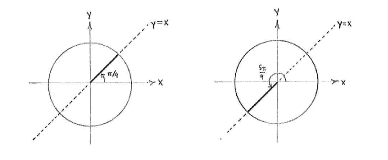
After drawing the unit circle and the line y=x, we see that there are two angles which satisfy these conditions, \displaystyle v={\pi }/{4}\; and \displaystyle v=\pi +{\pi }/{4}\;={5\pi }/{4}\;