Lösung 2.3:9b
Aus Online Mathematik Brückenkurs 1
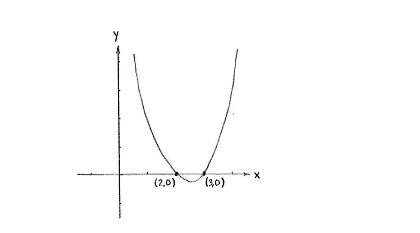
The points of intersection are those points on the curve which also lie on the x-axis, i.e. they are those points which satisfy both the equation of the curve \displaystyle y=x^{2}-5x+6 and the equation of the x-axis \displaystyle y=0,
This system of equations gives directly that \displaystyle y=0 and that \displaystyle x must satisfy the quadratic equation \displaystyle x^{2}-5x+6=0\,. By completing the square, we obtain that the left-hand side is
and this gives that the equation has solutions \displaystyle x=\tfrac{5}{2}\pm\tfrac{1}{2}, i.e. \displaystyle x=\tfrac{5}{2}-\tfrac{1}{2}=\tfrac{4}{2}=2 and \displaystyle x=\tfrac{5}{2}+\tfrac{1}{2}=\tfrac{6}{2}=3.
The intersection points are therefore (2,0) and (3,0).