Aus Online Mathematik Brückenkurs 1

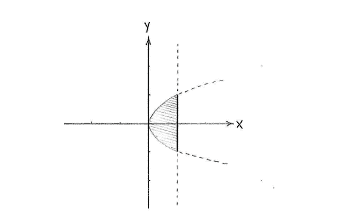
The expression \displaystyle \text{1}\ge x\ge \text{ }y^{\text{2}} means that we have a region which is defined by the two inequalities \displaystyle \text{1}\ge x\text{ } and \displaystyle x\ge \text{ }y^{\text{2}}. The first inequality gives us the region to the left of the line \displaystyle x=\text{1}. If the other inequality had been instead \displaystyle y=x^{\text{2}}, we would have a region above the parabola \displaystyle y=x^{\text{2}}, but in our case \displaystyle x and \displaystyle y have reversed roles, so the inequality \displaystyle x\ge \text{ }y^{\text{2}} defines the same type of parabolic region, but with the \displaystyle x - and \displaystyle y -axes having changed place.

Together, the inequalities define the region that is bordered on the left by the parabola and on the right by the line.