Aus Online Mathematik Brückenkurs 1

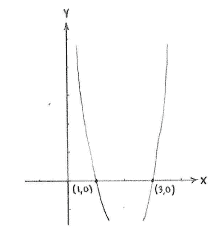
To determine all the points on the curve \displaystyle y=3x^{2}-12x+9 which also lie on the \displaystyle x -axis we substitute the equation of the \displaystyle x -axis i.e. \displaystyle y=0 in the equation of the curve and obtain that \displaystyle x must satisfy

\displaystyle 3x^{2}-12x+9=0

After dividing by \displaystyle 3 and completing the square the right-hand side is

\displaystyle x^{2}-4x+3=\left( x-2 \right)^{2}-2^{2}+3=\left( x-2 \right)^{2}-1

and thus the equation has solutions

\displaystyle x=2\pm 1, i.e. \displaystyle x=2-1=1 and \displaystyle x=2+1=3.

The points where the curve cut the \displaystyle x -axis are

\displaystyle \left( 1 \right.,\left. 0 \right) and \displaystyle \left( 3 \right.,\left. 0 \right)