Aus Online Mathematik Brückenkurs 1

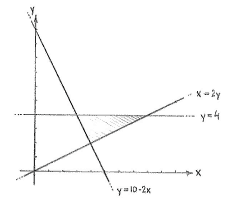
A first step is to draw the lines so that we get an overview of how the triangles look.

The corner points of the triangle are the intersection points of the lines and we obtain those more exactly by choosing the equations of the lines in pairs and solving the resulting system of equations.

\displaystyle \left\{ \begin{matrix} x=2y \\ y=4 \\ \end{matrix} \right.

\displaystyle \left\{ \begin{matrix} x=2y \\ y=10-2y \\ \end{matrix} \right. and \displaystyle \left\{ \begin{matrix} y=4 \\ y=10-2y \\ \end{matrix} \right.

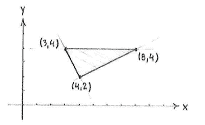
The first system of equations has the solution \displaystyle \left( x,y \right)=\left( \text{8},\text{4} \right), the other has the solution \displaystyle \left( x,y \right)=\left( \text{4},\text{2} \right)\text{ } and the third \displaystyle \left( x,y \right)=\left( \text{3},\text{4} \right).

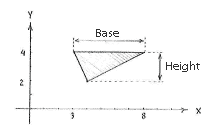
If we go back to the area of the triangle, which is given by the formula

Area= \displaystyle \frac{1}{2} (base)∙(height),

we are completely free to choose which edge of the triangle we take as the base. Because one of the edges is parallel with the x-axis, it seems best to choose that one as the base, since then we can easily read off the length of the base and the height as the difference in coordinates of the corner points.

The base is given as the horizontal distance between \displaystyle \left( \text{3},\text{4} \right)\text{ } and \displaystyle \text{ }\left( \text{8},\text{4} \right)

base= \displaystyle \text{8}-\text{3}=\text{5}

and we obtain the height in the same way as the difference in the \displaystyle y -direction between the base at \displaystyle y=\text{4 } and the corner point \displaystyle \left( \text{4},\text{2} \right),

height= \displaystyle \text{4}-\text{2}=\text{2}.

The area of the triangle is

Area = \displaystyle \frac{1}{2} (base)∙(height)= \displaystyle \frac{1}{2}\centerdot 5\centerdot 5

= \displaystyle \text{5} area units.