Aus Online Mathematik Brückenkurs 1

Let's write down the equation for a straight line as

\displaystyle y=kx+m

where \displaystyle k and \displaystyle m are constants which we shall determine.

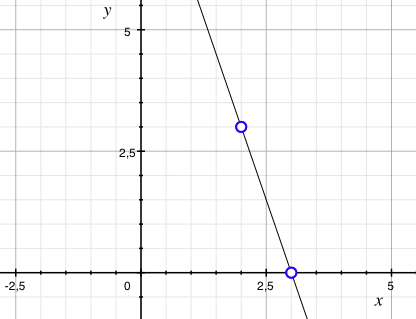
Since the points \displaystyle \left( 2 \right., \left. 3 \right) and \displaystyle \left( 3 \right., \left. 0 \right) should lie on the line, they must also satisfy the equation of the line,

\displaystyle 3=k\centerdot 2+m and \displaystyle 0=k\centerdot 3+m

If we take the difference between the equations, \displaystyle m disappears and we can work out the gradient \displaystyle k,

\displaystyle 3-0=k\centerdot 2+m-\left( k\centerdot 3+m \right)

\displaystyle 3=-k

Substituting this into the equation \displaystyle 0=k\centerdot 3+m then gives us a value for \displaystyle m,

\displaystyle m=-3k=-3\centerdot \left( -3 \right)=9

The equation of the line is thus \displaystyle y=-3x+9.

NOTE: To be completely certain that we have calculated correctly, we check that the points \displaystyle \left( 2 \right., \left. 3 \right) and \displaystyle \left( 3 \right., \left. 0 \right) satisfy the equation of the line:

\displaystyle \left( x \right., \left. y \right)=\left( 2 \right., \left. 3 \right): LHS= \displaystyle 3 and RHS= \displaystyle -3\centerdot 2+9=3

\displaystyle \left( x \right., \left. y \right)=\left( 3 \right., \left. 0 \right): LHS= \displaystyle 0 and LHS= \displaystyle -3\centerdot 3+9=0