Aus Online Mathematik Brückenkurs 1

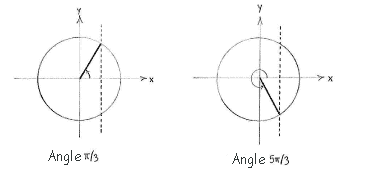
Die Gleichung \displaystyle \cos x= 1/2 hat die Lösung \displaystyle x=\pi/3 im ersten Quadrant, und die symmetrische Lösung \displaystyle x = 2\pi -\pi/3 = 5\pi/3 im vierten Quadrant.

Addieren wir einen Multipel von \displaystyle 2\pi zu diesen Winkeln, erhalten wir die allgemeine Lösung,

\displaystyle x = \frac{\pi}{3}+2n\pi\qquad\text{und}\qquad x = \frac{5\pi }{3}+2n\pi\,,