Aus Online Mathematik Brückenkurs 1

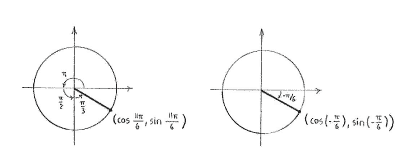
Wir schreiben \displaystyle 11\pi/6 wie

\displaystyle \frac{11\pi}{6} = \frac{6\pi+3\pi+2\pi}{6} = \pi + \frac{\pi}{2} + \frac{\pi}{3}

und sehen dass der Winkel im vierten Quadrant liegt.

Wir sehen auch dass der winkel denselben Punkt am Einheitskreis entspricht, wie der Winkel \displaystyle \cos (-\pi/6), den wir schon in der Übung 4.2:3f berechnet haben. Also haben wir

\displaystyle \cos\frac{11\pi}{6} = \cos\Bigl(-\frac{\pi}{6}\Bigr) = \frac{\sqrt{3}}{2}\,\textrm{.}