Lösung 4.4:3d
Aus Online Mathematik Brückenkurs 1
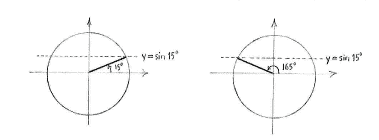
First, we observe from the unit circle that the equation has two solutions for \displaystyle 0^{\circ}\le 3x\le 360^{\circ}\,,
| \displaystyle 3x = 15^{\circ}\qquad\text{and}\qquad 3x = 180^{\circ} - 15^{\circ} = 165^{\circ}\,\textrm{.} |
This means that all of the equation's solutions are
| \displaystyle 3x = 15^{\circ} + n\cdot 360^{\circ}\qquad\text{and}\qquad 3x = 165^{\circ} + n\cdot 360^{\circ}\,, |
for all integers n, i.e.
| \displaystyle x = 5^{\circ} + n\cdot 120^{\circ}\qquad\text{and}\qquad x = 55^{\circ} + n\cdot 120^{\circ}\,\textrm{.} |