Aus Online Mathematik Brückenkurs 1

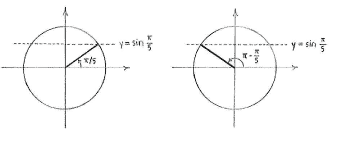
We see directly that \displaystyle x = \pi/5 is a solution to the equation, and using the unit circle we can also draw the conclusion that \displaystyle x = \pi - \pi/5 = 4\pi/5 is the only other solution between \displaystyle 0 and \displaystyle 2\pi\,.

We obtain all solutions to the equation when we add integer multiples of \displaystyle 2\pi\, ,

\displaystyle x = \frac{\pi}{5} + 2n\pi\qquad\text{and}\qquad x = \frac{4\pi}{5} + 2n\pi\,,

where n is an arbitrary integer.