Lösung 4.2:7
Aus Online Mathematik Brückenkurs 1
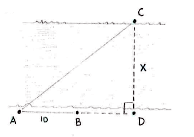
If we extend the line AB to a point D opposite C, we will get the right-angled triangle shown below, where the distance x between C and D is the desired distance.
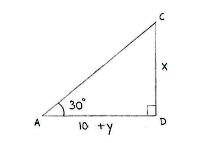
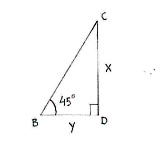
The information in the exercise can be summarized by considering the two triangles ACD and BCD, and setting up relations for the tangents that the angles 30° and 45° gives rise to,
| 
| |
| \displaystyle \begin{align} x &= (10+y)\tan 30^{\circ}\\[5pt] &= (10+y)\frac{1}{\sqrt{3}}\end{align} | \displaystyle \begin{align} x &= y\cdot\tan 45^{\circ}\\[5pt] &= y\cdot 1\end{align} |
where y is the distance between B and D.
The second relation above gives that \displaystyle y=x and substituting this into the first relation gives
Multiplying both sides by \displaystyle \sqrt{3} gives
moving all the x-terms to the left-hand side gives
The answer is