Lösung 2.2:6b
Aus Online Mathematik Brückenkurs 1
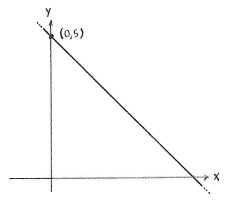
Because the point of intersection lies on both lines, it must satisfy the equations of both lines
where \displaystyle x=0 is the equation of the y-axis. Substituting the second equation, \displaystyle x=0, into the first equation gives \displaystyle y=-0+5=5. This means that the point of intersection is (0,5).