Lösung 2.2:5a
Aus Online Mathematik Brückenkurs 1
Let's write down the equation for a straight line as
where k and m are constants which we shall determine.
Since the points (2,3) and (3,0) should lie on the line, they must also satisfy the equation of the line,
If we take the difference between the equations, m disappears and we can work out the slope k,
Substituting this into the equation \displaystyle 0=k\centerdot 3+m then gives us a value for m,
The equation of the line is thus \displaystyle y=-3x+9.
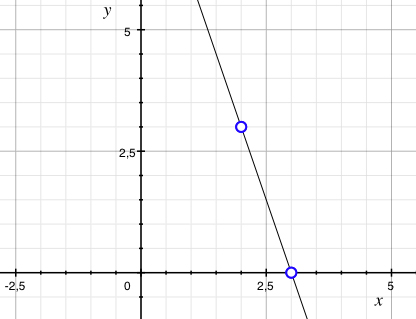
Note. To be completely certain that we have calculated correctly, we check that the points (2,3) and (3,0) satisfy the equation of the line:
- (x,y) = (2,3): \displaystyle \text{LHS} = 3\ and \displaystyle \ \text{RHS} = -3\cdot 2+9 = 3\,.
- (x,y) = (3,0): \displaystyle \text{LHS} = 0\ and \displaystyle \ \text{LHS} = -3\cdot 3+9 = 0\,.
