Lösung 4.4:5c
Aus Online Mathematik Brückenkurs 1
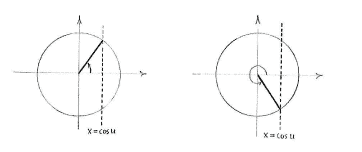
For a fixed value of \displaystyle u, an equality of the form
\displaystyle \cos u=\cos v
is satisfied by two angles
\displaystyle v
in the unit circle:
\displaystyle v=u
and
\displaystyle v=-u
This means that all angles \displaystyle v which satisfy the equality are
\displaystyle v=u+2n\pi
and
\displaystyle v=-u+2n\pi
where
\displaystyle n\text{ }
is an arbitrary integer.
Therefore, the equation
\displaystyle \cos 5x=\cos \left( x+{\pi }/{5}\; \right)
has the solutions
\displaystyle 5x=x+\frac{\pi }{5}+2n\pi
or
\displaystyle 5x=-x-\frac{\pi }{5}+2n\pi
If we collect \displaystyle x\text{ } onto one side, we end up with
\displaystyle \left\{ \begin{array}{*{35}l}
x=\frac{\pi }{20}+\frac{1}{2}n\pi \\
x=-\frac{\pi }{30}+\frac{1}{3}n\pi \\
\end{array} \right.
(
\displaystyle n\text{ }
an arbitrary integer).