Aus Online Mathematik Brückenkurs 1

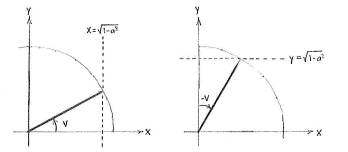
The expression for the angle \displaystyle {\pi }/{2}\;-v differs from \displaystyle {\pi }/{2}\; by as much as \displaystyle -v\text{ } differs from \displaystyle 0. This means that \displaystyle {\pi }/{2}\; makes the same angle with the positive \displaystyle y -axis as \displaystyle -v\text{ } makes with the positive \displaystyle x -axis.

Angle \displaystyle v angle \displaystyle \pi -v

Therefore, the angle \displaystyle {\pi }/{2}\;-v has a \displaystyle y -coordinate which is equal to the \displaystyle x -coordinate for the angle \displaystyle v, i.e.

\displaystyle \sin \left( {\pi }/{2}\;-v \right)=\cos v

and from exercise c, we know that \displaystyle \cos v=\sqrt{1-a^{2}}

\displaystyle \sin \left( \frac{\pi }{2}-v \right)=\sqrt{1-a^{2}}