Lösung 4.2:8
Aus Online Mathematik Brückenkurs 1
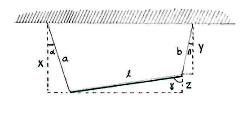
We start by drawing three auxiliary triangles, and calling the three vertical sides \displaystyle x,\ y and \displaystyle z, as shown in the figure.
Using the definition of cosine, we can work out \displaystyle x\text{ } and \displaystyle y from
\displaystyle x=a\cos \alpha
\displaystyle y=b\cos \beta
and, for the same reason, we know that \displaystyle z\text{ } satisfies the relation
\displaystyle z=l\cos \gamma
In addition, we know that the lengths
\displaystyle x,\ y
and
\displaystyle z
satisfy the equality
\displaystyle z=x-y
If we substitute in the expressions for
\displaystyle x,\ y
and
\displaystyle z, we obtain the trigonometric equation
\displaystyle l\cos \gamma =a\cos \alpha -b\cos \beta
where
\displaystyle \gamma
is the only unknown.