Lösung 4.1:4a
Aus Online Mathematik Brückenkurs 1
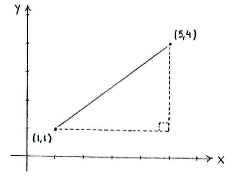
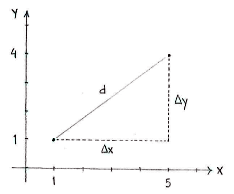
If we draw in the points in a coordinate system, we can see the line between the points as the hypotenuse in an imaginary right-angled triangle, where the opposite and adjacent are parallel with the \displaystyle x - and \displaystyle y -axes.
In this triangle, it is easy to measure the lengths of the opposite and the adjacent, which are simply the distances between the points in the \displaystyle x - \displaystyle y -directions.
Using Pythagoras' theorem, we can then calculate the length of the hypotenuse, which is also the distance between the points:
\displaystyle \begin{align}
& d=\sqrt{\left( \Delta x \right)^{2}+\left( \Delta y \right)^{2}}=\sqrt{4^{2}+3^{2}} \\
& =\sqrt{16+9}=\sqrt{25}=5 \\
\end{align}
NOTE: In general, the distance between two points
\displaystyle \left( x \right.,\left. y \right)
and
\displaystyle \left( a \right.,\left. b \right)
is given by the formula
\displaystyle d=\sqrt{\left( x-a \right)^{2}+\left( y-b \right)^{2}}