Lösung 4.4:3c
Aus Online Mathematik Brückenkurs 1
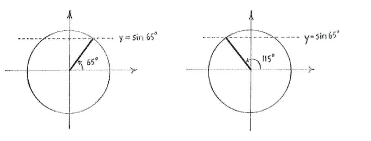
Falls wir \displaystyle x + 40^{\circ} als unbekannte Variable betrachten, haben wir eine einfache trigonometrische Gleichung wie vorher. Wir sehen, dass es im Intervall \displaystyle 0^{\circ}\le x+40^{\circ}\le 360^{\circ} zwei Lösungen gibt, nämlich \displaystyle x+40^{\circ} = 65^{\circ} und die symmetrische Lösung \displaystyle x + 40^{\circ} = 180^{\circ} - 65^{\circ} = 115^{\circ}\,.
Die allgemeine Lösung ist damit
| \displaystyle x + 40^{\circ} = 65^{\circ} + n\cdot 360^{\circ}\qquad\text{und}\qquad x + 40^{\circ} = 115^{\circ} + n\cdot 360^{\circ} |
Also erhalten wir die Lösungen
| \displaystyle x = 25^{\circ} + n\cdot 360^{\circ}\qquad\text{und}\qquad x=75^{\circ} + n\cdot 360^{\circ}\,\textrm{.} |