Aus Online Mathematik Brückenkurs 1

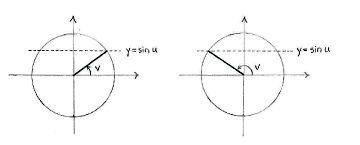
Betrachten wir die Gleichung

\displaystyle \sin u = \sin v,

(*)

wobei u eine Konstante ist, gibt es zwei Lösungen für diese Gleichung, nämlich

\displaystyle v=u\qquad\text{und}\qquad v=\pi-u\,\textrm{.}

(Die einzige Ausnahme ist, wenn \displaystyle u = \pi/2 oder \displaystyle u=3\pi/2, da in diesen Fällen \displaystyle u und \displaystyle \pi-u dieselben Winkel sind)

Wir erhalten die allgemeine Lösung, indem wir ein Vielfaches von \displaystyle 2\pi zur Lösung addieren:

\displaystyle v = u+2n\pi\qquad\text{und}\qquad v = \pi-u+2n\pi\,.

Für unsere Gleichung

\displaystyle \sin 3x = \sin x

erhalten wir die Lösungen

\displaystyle 3x = x+2n\pi\qquad\text{oder}\qquad 3x = \pi-x+2n\pi\,\textrm{.}

Lösen wir x, erhalten wir

\displaystyle \left\{\begin{align} x &= 0+n\pi\,,\\[5pt] x &= \frac{\pi}{4}+\frac{n\pi}{2}\,\textrm{.} \end{align}\right.