Aus Online Mathematik Brückenkurs 1

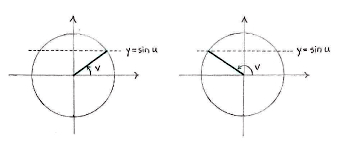
If we consider for a moment the equality

\displaystyle \sin u = \sin v

(*)

where u has a fixed value, there are usually two angles v in the unit circle which ensure that the equality holds,

\displaystyle v=u\qquad\text{and}\qquad v=\pi-u\,\textrm{.}

(The only exception is when \displaystyle u = \pi/2 or \displaystyle u=3\pi/2, in which case \displaystyle u and \displaystyle \pi-u correspond to the same direction and there is only one angle v which satisfies the equality.)

We obtain all the angles v which satisfy (*) by adding multiples of \displaystyle 2\pi,

\displaystyle v = u+2n\pi\qquad\text{and}\qquad v = \pi-u+2n\pi\,,

where n is an arbitrary integer.

If we now go back to our equation

\displaystyle \sin 3x = \sin x

the reasoning above shows that the equation is only satisfied when

\displaystyle 3x = x+2n\pi\qquad\text{or}\qquad 3x = \pi-x+2n\pi\,\textrm{.}

If we make x the subject of each equation, we obtain the full solution to the equation,

\displaystyle \left\{\begin{align} x &= 0+n\pi\,,\\[5pt] x &= \frac{\pi}{4}+\frac{n\pi}{2}\,\textrm{.} \end{align}\right.