Lösung 4.2:8
Aus Online Mathematik Brückenkurs 1
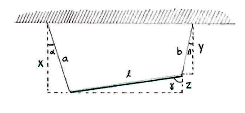
We start by drawing three auxiliary triangles, and calling the three vertical sides x, y and z, as shown in the figure.
Using the definition of cosine, we can work out x and y from
| \displaystyle \begin{align}
x &= a\cos \alpha\,,\\[3pt] y &= b\cos \beta\,, \end{align} |
and, for the same reason, we know that z satisfies the relation
| \displaystyle z=\ell\cos \gamma\,\textrm{.} |
In addition, we know that the lengths x, y and z satisfy the equality
| \displaystyle z=x-y\,\textrm{.} |
If we substitute in the expressions for x, y and z, we obtain the trigonometric equation
| \displaystyle \ell\cos \gamma = a\cos \alpha -b\cos \beta\,\textrm{,} |
where \displaystyle \gamma is the only unknown.