4.1 Winkel und Kreise

Aus Online Mathematik Brückenkurs 1

Wechseln zu: Navigation, Suche
 

Vorlage:Selected tab Vorlage:Not selected tab

 

Contents:

  • Various angle measures (degrees, radians and revolutions)
  • The Pythagorean theorem
  • Formula for distance in the plane
  • Equation of a circle

Learning outcomes:

After this section, you will have learned :

  • To convert between degrees, radians and revolutions.
  • To calculate the area and circumference of sectors of a circle.
  • The concepts of right-angled triangles including its legs and hypotenuse.
  • To formulate and use the Pythagorean theorem.
  • To calculate the distance between two points in the plane.
  • To sketch circles by completing the square in their equations.
  • The concepts of unit circle, tangent, radius, diameter, circumference, chord and arc.
  • To solve geometric problems that contain circles.

Angle measures

There are several different units for measuring angles, which are used in different contexts. The two most common within mathematics are degrees and radians.

  • Degrees. If a complete revolution is divided into 360 parts, then each part is called 1 degree. Degrees are designated by \displaystyle {}^\circ.
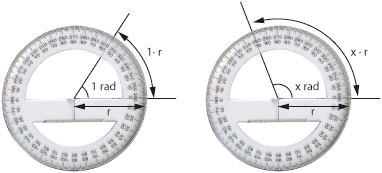
  • Radians. Another way to measure an angle, is to use the length of the arc which subtends the angle in relation to the radius as a measure of the angle. This unit is called radian. A revolution is \displaystyle 2\pi radians as the circumference of a circle is \displaystyle 2\pi r, where \displaystyle r is the radius of the circle.


A complete revolution is \displaystyle 360^\circ or \displaystyle 2\pi radians which means Vorlage:Displayed math These conversion relations can be used to convert between degrees and radians.

Example 1

  1. \displaystyle 30^\circ = 30 \cdot 1^\circ = 30 \cdot \frac{\pi}{180}\ \mbox{ radians } = \frac{\pi}{6}\ \mbox{ radians }
  2. \displaystyle \frac{\pi}{8}\ \mbox { radians } = \frac{\pi}{8} \cdot (1 \; \mbox{radians}\,) = \frac{\pi}{8} \cdot \frac{180^\circ}{\pi} = 22{,}5^\circ

In some contexts, it may be useful to talk about negative angles and angles greater than 360°. This means that the same direction can be designated by different angles that differ from each other by an integral number of revolutions.

[Image]

Example 2

  1. The angles \displaystyle -55^\circ and \displaystyle 665^\circ indicate the same direction because Vorlage:Displayed math
  2. The angles \displaystyle \frac{3\pi}{7} and \displaystyle -\frac{11\pi}{7} indicate the same direction because Vorlage:Displayed math
  3. The angles \displaystyle 36^\circ and \displaystyle 216^\circ do not specify the same direction, but opposite directions since Vorlage:Displayed math


Formula for distance in the plane

The theorem of Pythagoras is one of the most famous theorems in mathematics and says that in a right-angled triangle with the legs \displaystyle a and \displaystyle b, and the hypotenuse \displaystyle c then

The Pythagorean theorem:

Vorlage:Displayed math

4.1 - Figure - The Pythagorean theorem

Example 3

The triangle on the right is

Vorlage:Displayed math and therefore hypotenuse \displaystyle c is equal to Vorlage:Displayed math

[Image]

The Pythagorean theorem can be used to calculate the distance between two points in a coordinate system.

Formula for distance:

The distance \displaystyle d between two points with coordinates \displaystyle (x,y) and \displaystyle (a,b) is Vorlage:Displayed math

The line joining the points is the hypotenuse of a triangle whose legs are parallel to the coordinate axes.

4.1 - Figure - The distance formula

The legs of the triangle have lengths equal to the difference in the x- and y-directions of the points, that is \displaystyle |x-a| and \displaystyle |y-b|. The Pythagorean theorem then gives the formula for the distance.

Example 4

  1. The distance between \displaystyle (1,2) and \displaystyle (3,1) is Vorlage:Displayed math
  2. The distance between \displaystyle (-1,0) and \displaystyle (-2,-5) is Vorlage:Displayed math


Circles

A circle consists of all the points that are at a given fixed distance \displaystyle r from a point \displaystyle (a,b).

4.1 - Figure - Circle


The distance \displaystyle r is called the circle´s radius and the point \displaystyle (a,b) is its centre. The figure below shows the other important concepts.

4.1 - Figure - Diameter 4.1 - Figure - Tangent 4.1 - Figure - The chord of a circle 4.1 - Figure - Secant
Diameter Tangent Chord Secant

[Image]

4.1 - Figure - Circumference 4.1 - Figure - Sector of a circle 4.1 - Figure - Segment of a circle
Arc of a circle circumference sector of a circle segment of a circle

Example 5

A sector of a circle is given in the figure on the right.
  1. Determine its arc length .

    The central angle \displaystyle 50^\circ is in radians Vorlage:Displayed math

[Image]

  1. The way radians have been defined means that the arc length is the radius multiplied by the angle measured in radians, Vorlage:Displayed math
  1. Determine the area of the circle segment.

    The circle segment´s share of the entire circle is Vorlage:Displayed math and this means that its area is \displaystyle \frac{5}{36} parts of the circle area, which is \displaystyle \pi r^2 = \pi 3^2 = 9\pi, i.e. Vorlage:Displayed math

A point \displaystyle (x,y) lies on the circle that has its centre at \displaystyle (a,b) and radius \displaystyle r, if its distance from the centre is equal to \displaystyle r. This condition can be formulated with the distance formula as

Circle equation:

Vorlage:Displayed math

4.1 - Figure - Equation of a circle

Example 6

  1. \displaystyle (x-1)^2 + (y-2)^2 = 9\quad is the equation for a circle with its centre at \displaystyle (1,2) and radius \displaystyle \sqrt{9} = 3.
4.1 - Figure - The equation (x - 1)² + (y - 2)² = 9
  1. \displaystyle x^2 + (y-1)^2 = 1\quad can be written as \displaystyle (x-0)^2 + (y-1)^2 = 1 and is the equation of a circle with its centre at \displaystyle (0,1) and having a radius \displaystyle \sqrt{1} = 1.
4.1 - Figure - The equation x² + (y - 1)² = 1
  1. \displaystyle (x+1)^2 + (y-3)^2 = 5\quad can be written as \displaystyle (x-(-1))^2 + (y-3)^2 = 5 and is the equation of a circle with its centre at \displaystyle (-1,3) and having a radius \displaystyle \sqrt{5} \approx 2\textrm{.}236.
4.1 - Figure - The equation (x + 1)² + (y - 3)² = 5

Example 7

  1. Does the point \displaystyle (1,2) lie on the circle \displaystyle (x-4)^2 +y^2=13?

    Inserting the coordinates of the point \displaystyle x=1 and \displaystyle y=2 in the circle equation, we have that Vorlage:Displayed math Since the point satisfies the circle equation it lies on the circle.
    4.1 - Figure - The equation (x - 4)² + y² = 13
  2. Determine the equation for the circle that has its centre at \displaystyle (3,4) and goes through the point \displaystyle (1,0).

    Since the point \displaystyle (1,0) lies on the circle, the radius of the circle must be equal to the distance of the point from \displaystyle (1,0) to the centre \displaystyle (3,4). The distance formula gives that this distance is Vorlage:Displayed math The circle equation is therefore Vorlage:Displayed math
    4.1 - Figure - The equation (x - 3)² + (y - 4)² = 20


Example 8

Determine the centre and radius of the circle with equation \displaystyle \ x^2 + y^2 – 2x + 4y + 1 = 0.


Let us try to write the equation of the circle in the form Vorlage:Displayed math because then we can directly read from this that the midpoint is \displaystyle (a,b) and the radius is \displaystyle r.

Start by completing the square for the terms containing \displaystyle x on the left-hand side Vorlage:Displayed math (the underlined terms shows the terms involved).

Complete the square for the terms containing \displaystyle y Vorlage:Displayed math

The left-hand side is equal to Vorlage:Displayed math

and moving over the 4 to to the right-hand side we get the equation Vorlage:Displayed math

We can interpret this as follows: The centre is at \displaystyle (1,-2) and the radius is \displaystyle \sqrt{4}= 2.

4.1 - Figure - The equation x² + y² - 2x + 4y + 1 = 0


Exercises

Study advice

The basic and final tests

After you have read the text and worked through the exercises, you should do the basic and final tests to pass this section. You can find the link to the tests in your student lounge.


Keep in mind that:


Reviews

For those of you who want to deepen your studies or need more detailed explanations consider the following references:

Learn more about Pythagoras theorem in English Wikipedia

Read more in Mathworld about the circle


Useful web sites

Interactive experiments: the sine and cosine on the unit circle (Flash)

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/4.1_Winkel_und_Kreise“