Aus Online Mathematik Brückenkurs 1

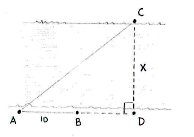
If we extend the line AB to a point D opposite C, we will get the right-angled triangle shown below, where the distance x between C and D is the desired distance.

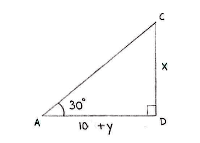
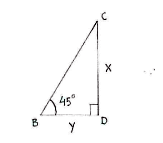
The information in the exercise can be summarized by considering the two triangles ACD and BCD, and setting up relations for the tangents that the angles 30° and 45° gives rise to,

\displaystyle \begin{align} x &= (10+y)\tan 30^{\circ}\\[5pt] &= (10+y)\frac{1}{\sqrt{3}}\end{align}		\displaystyle \begin{align} x &= y\cdot\tan 45^{\circ}\\[5pt] &= y\cdot 1\end{align}

where y is the distance between B and D.

The second relation above gives that \displaystyle y=x and substituting this into the first relation gives

\displaystyle x = (10+x)\frac{1}{\sqrt{3}}\,\textrm{.}

Multiplying both sides by \displaystyle \sqrt{3} gives

\displaystyle \sqrt{3}x=10+x

moving all the x-terms to the left-hand side gives

\displaystyle (\sqrt{3}-1)x = 10\,\textrm{.}

The answer is

\displaystyle x = \frac{10}{\sqrt{3}-1}\ \text{m}\approx 13\textrm{.}6\ \text{m.}