Aus Online Mathematik Brückenkurs 1

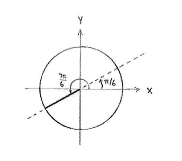
If we write the angle \displaystyle \frac{7\pi}{6} as

\displaystyle \frac{7\pi}{6} = \frac{6\pi+\pi}{6} = \pi + \frac{\pi }{6}

we see that the angle \displaystyle 7\pi/6 on the unit circle is in the third quadrant and makes an angle \displaystyle \pi/6 with the negative x-axis.

Geometrically, \displaystyle \tan (7\pi/6) is defined as the slope of the line having an angle \displaystyle 7\pi/6 and, because this line has the same slope as the line having angle \displaystyle \pi/6, we have that

\displaystyle \tan\frac{7\pi}{6} = \tan\frac{\pi}{6} = \frac{\sin\dfrac{\pi }{6}}{\cos\dfrac{\pi }{6}} = \frac{\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}}\,\textrm{.}