Lösung 4.2:4b
Aus Online Mathematik Brückenkurs 1
We start by subtracting \displaystyle 2\pi from \displaystyle 11\pi/3, so that we get an angle between \displaystyle 0 and \displaystyle 2\pi . This doesn't change the cosine value
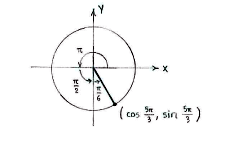
Then, by rewriting \displaystyle 5\pi/3 as a sum of \displaystyle \pi- and \displaystyle \pi/2-terms,
we see that \displaystyle 5\pi/3 is an angle in the fourth quadrant which makes an angle \displaystyle \pi/6 with the negative y-axis.
With the help of an auxiliary triangle and a little trigonometry, we can determine the coordinates for the point on a unit circle which corresponds to the angle \displaystyle 5\pi/3\,.
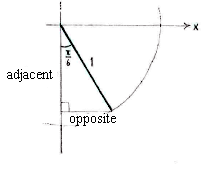
| \displaystyle \begin{align}\text{opposite} &= 1\cdot\sin\frac{\pi}{6} = \frac{1}{2}\\[5pt] \text{adjacent} &= 1\cdot\cos\frac{\pi}{6} = \frac{\sqrt{3}}{2}\end{align} |
The point has coordinates \displaystyle (1/2,-\sqrt{3}/2) and