Lösung 4.4:2f
Aus Online Mathematik Brückenkurs 1
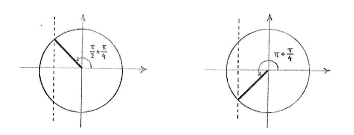
Using the unit circle shows that the equation \displaystyle \text{cos 3}x=-\frac{1}{\sqrt{2}} has two solutions for \displaystyle 0\le \text{3}x\le \text{2}\pi ,
\displaystyle 3x=\frac{\pi }{2}+\frac{\pi }{4}=\frac{3\pi }{4}
and
\displaystyle 3x=\pi +\frac{\pi }{4}=\frac{5\pi }{4}
We obtain the other solutions by adding multiples of \displaystyle 2\pi ,
\displaystyle 3x=\frac{3\pi }{4}+2n\pi
and
\displaystyle 3x=\frac{5\pi }{4}+2n\pi
i.e.
\displaystyle x=\frac{\pi }{4}+\frac{2}{3}n\pi
and
\displaystyle x=\frac{5\pi }{12}+\frac{2}{3}n\pi
where
\displaystyle n
is an arbitrary integer.